通過萬用表了解信號如何影響測量質量

       讓我們來看萬用表幾個不同的信號，首先是正弦波。純正弦波的波峰因數為1.414，峰值響應儀表僅需定標Vpk值就能提供精確的有效值。如果Vpk值是500mV，我們估計有效值大約為350至357mV(此范圍考慮了所用信號發生器的不精確度)。不出所料，真有效值儀表獲得的信號讀數為353.53mV。價格較低的平均值響應儀表得到的信號讀數為351mV。

　　與純正弦波不同，三角波擁有部分高頻能量，因此波峰因數為1.732，完全在意料之內。將峰值除以波峰因數，得出預計的有效值為大約 290 mV。現在，平均響應儀表開始出現問題，其信號讀數為276mV，與真有效值儀表288.68mV 的讀數相比，出現4%的誤差。

　　現在讓我們看一下脈沖串，此處的波峰因數取決于占空比。您可以通過下列公式獲得與波峰因數接近的近似值：

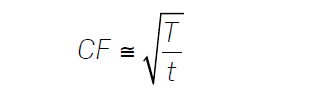
　　其中：

　　CF = 波峰因數

　　T = 波形周期

　　t = 此周期中有信號的部分

　　它也等于占空比倒數的平方根。因此，以圖1中的脈沖串為例，其占空比為2%，波峰因數就是50的平方根或 7.071。

　　計算正弦波和三角波的有效值相當簡單;有效值等于Vpk除以波峰因數。然而，計算脈沖串的交流有效值則稍為復雜：

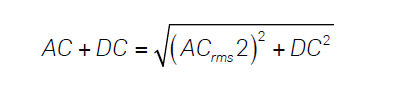
　　使用此公式，圖1中具有2%占空比的2Vpk 脈沖串的理論有效值約為280mV。即使在此例中，其有效值已經超出了指定的性能范圍，但真有效值儀表讀數為275.9mV。另一方面，平均響應儀表讀數為73mV，誤差達到74%。這是一個極端的例子，但是能夠讓您清楚地了解高波峰因數會給您的測量帶來什么影響。

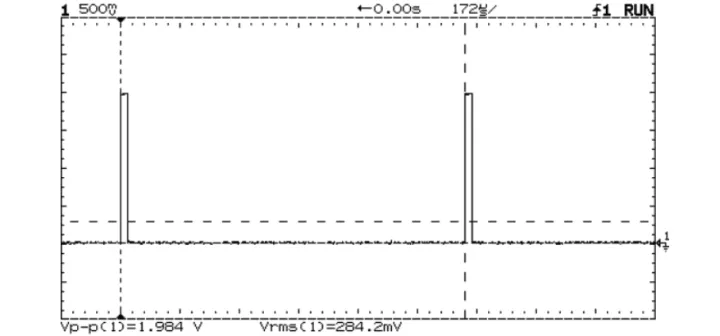
　　圖 1. 測量低占空比脈沖串的有效值

　　讓我們再看看另一個波形--圖2中顯示的包含噪聲的雜亂正弦波。真有效值儀表的讀數為348.9 mV，此結果接近數字示波器測量所得的345mV。平均響應儀表將該值設為273mV，誤差超過20%。這一誤差是由平均響應儀表有限的帶寬所致。信號包含高頻能量，而平均響應儀表未將其考慮在內。

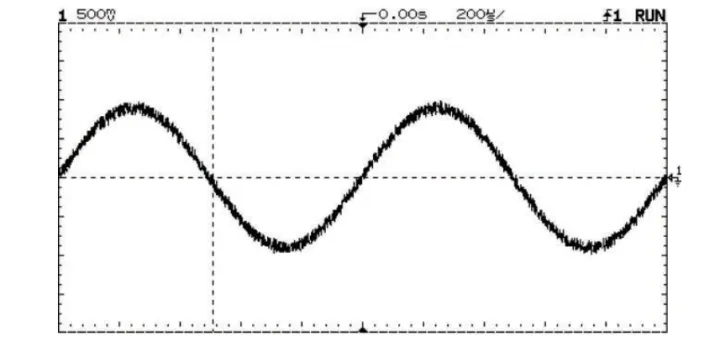
　　圖 2. 測量噪聲正弦波的有效值

     以上就是通過萬用表了解信號如何影響測量質量的介紹，更多信息歡迎登錄安泰測試官網進行了解。